9064. Old man and chessboard

 

Kratos has travelled to many different places during his journey. So, today he wandered into a small village, where he was sheltered by a gray-haired old man, fed and gave a place for an overnight stay. Instead, the old man asked only one thing – to make a chessboard for him, because he loves this game so much.

The old man has n white and m black squares 1 * 1, out of which he wants to make not an ordinary board 8 * 8, but the largest possible, which firstly will be square, and secondly will have a checkerboard coloring, that is, where any two adjacent cells on the side will be of different colors (while the corner cells can be either white or black, in contrast to the usual chessboard). Kratos did not quite understand why the old man needed such a board, but did not argue, and set to work. However, our titanium has very bad mathematics, so finding the length of the side of the square, which should eventually turn out, turned out to be an impossible task for him, and he turned to you for help. Help him – find the maximum length of a chessboard, which can be made up of existing squares.

 

Input. Two integers n and m (0 ≤ n, m ≤ 109) – the number of white and black squares respectively. It is guaranteed that n + m > 0.

 

Output. Print the length of the side of the maximum possible square having a checkerboard coloring, which can be made up of the old man’s squares. You do not need to use all squares.

 

Sample input 1

Sample output 1

8 9

4

 

 

Sample input 2

Sample output 2

15 12

5

 

 

SOLUTION

full search - mathematics

 

Algorithm analysis

A square containing n + m cells has side length at most . Let x be the side length of the square.

If x is even, then such square has the same number of black and white cells, and it equals to x2 / 2. If x2 / 2 ≤ n and x2 / 2 ≤ m, then a square with side x can be made from the old man’s squares.

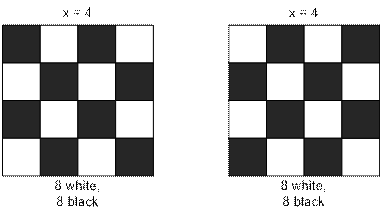
If x is odd, then the number of black and white cells in such a square differs by 1 and, depending on the color of the painting of one of the corners, can be equal to:

·        (x2 – 1) / 2 white cells and (x2 + 1) / 2 black cells;

·        (x2 – 1) / 2 black cells and (x2 + 1) / 2 white cells;

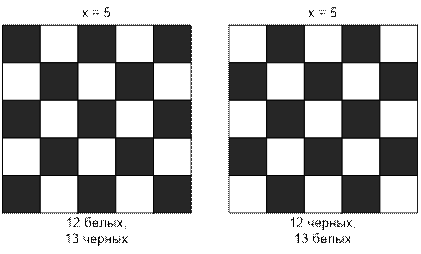
If the number of white and black squares is at most n and m, then a square with side x can be made.

Iterate over the value of x from  down to 1 and print the first such number x for which the required square exists.

 

Algorithm realization

Read the input data.

 

scanf("%d %d", &n, &m);

x = sqrt(n + m);

 

Iterate over the possible length of the side of the square.

 

for (i = x; i > 0; i--)

{

  if (i % 2 == 0)

  {

 

The length of the side of the square i is even. If there are i2 / 2 white and black squares available, then the answer is found.

 

    q = i * i / 2;

    if (n >= q && m >= q) break;

  }

  else

  {

 

The side length of the square i is odd. If there are (x2 – 1) / 2 white and (x2 + 1) / 2 black squares or (x2 – 1) / 2 black and (x2 + 1) / 2 white squares, then the answer is found.

 

    q = (i * i - 1) / 2;

    if (n >= q && m >= q + 1) break;

    if (n >= q + 1 && m >= q) break;

  }

}

 

Print the answer.

 

printf("%d\n", i);

 

Algorithm realization – formula

Read the input data. Swap n and m so that n ≤ m.

 

scanf("%d %d", &n, &m);

if (n > m) swap(n, m); // n <= m

 

Let the side x of the square is even. Since x2 / 2 ≤ n, then . Find  and check if x is even. If x is odd, decrease it by 1. The checkerboard with side x can be made.

 

x = int(sqrt(2 * n));

if (x % 2 == 1) x--;

res = x;

 

Let the side x of the square is odd. The number of white and black squares must differ by 1. If n = m, decrease n by 1.

 

if (n == m) n--;

 

The inequality takes place: (x2 – 1) / 2  ≤ n, that is . Find  and check if x is odd. If x is even, decrease it by 1. The checkerboard with side x can be made.

 

x = int(sqrt(2 * n + 1));

if (x % 2 == 0) x--;

if (x > res) res = x;

 

Print the answer.

 

printf("%d\n", res);